向量x乘矩阵方法？写出设计矩阵x

文章目录

向量x乘矩阵方法？

向量与矩阵的乘法可以通过以下步骤进行：

如果矩阵的列数与向量的长度相同，则可以将向量逐行逐列地乘到每一个矩阵元素上。

如果向量的长度与矩阵的行数相同，则可以将向量逐行地乘到每一个矩阵元素上。

如果矩阵的列数与向量的长度不同，或者向量的长度与矩阵的行数不同，则无法直接进行乘法运算。

例如，假设有一个 m×n 的矩阵 A 和一个 n×p 的矩阵 B，那么可以通过以下步骤将 A 与 B 相乘：

将 A 的每一行都与 B 的每一列相乘，得到一个新的 m×p 的矩阵 C。

对于 C 中的每一个元素 C_ij，计算公式为：C_ij = Σ_k=1^n (A_ik * B_kj)。

其中，i 表示行号，j 表示列号，k 表示中间的变量号。

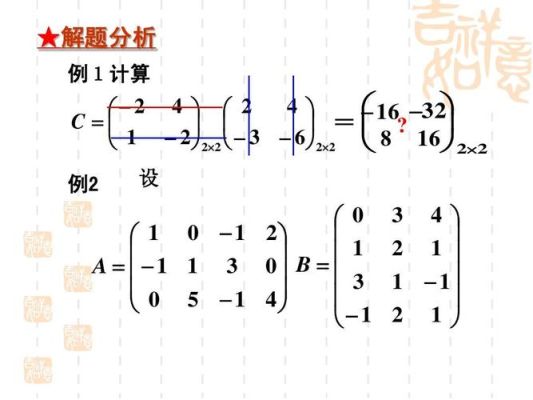
向量乘以矩阵的方法是按照矩阵乘法的规则进行的。设矩阵A的大小为m×n，向量x的大小为n×1，那么它们的乘积结果是一个m×1的向量。

具体来说，就是将矩阵A的每一行与向量x相乘，然后将所得结果相加得到最终结果。

向量是一个一行n列（或n行一列）的特殊矩阵,适用于矩阵的运算规则.行向量乘以矩阵的话用行向量乘以矩阵的每一列,矩阵乘以列向量的话用矩阵的每一行乘以列向量

向量是一个一行n列（或n行一列）的特殊矩阵,适用于矩阵的运算规则.行向量乘以矩阵的话用行向量乘以矩阵的每一列,矩阵乘以列向量的话用矩阵的每一行乘以列向量

关于直线y=x对称的矩阵？

将x和y对换 再把y用x表示出来 若与原式相同则函数关于y=x对称

若一个函数的图像关于直线y=x对称，则有y=f(x)及x=f(y)。

一般来说，设函数y=f(x)(x∈A)的值域是C，若找得到一个函数g(y)在每一处g(y)都等于x，这样的函数x= g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数，记作y=f^(-1)(x) 。

反函数y=f ^(-1)(x)的定义域、值域分别是函数y=f(x)的值域、定义域。最具有代表性的反函数就是对数函数与指数函数

例如：y=x+1

关于y=x对称，即x=y-1，然后交换x，y，得y=x-1

y=x+1关于直线y=x对称的方程为y=x-1

函数转换为反函数步骤：

1、确定原函数的值域。

2、 解方程解出x。

x的转置矩阵怎么求？

X是一个3×1矩阵，X'是1×3矩阵，XX'是一个3×3矩阵，X'X是一个1×1的矩阵，实际上，它的数目等于的标量积两个向量。 设X =（ABC）“，则X'=（ABC） 一^ 2 AB AC XX'= BA B ^ 2约，X'X = A ^ 2 + B ^ 2 + C ^ 2， CA CB C 1-4 2 由于已知的XX'，从而使矩阵X'X XX'主对角线和数字。

对于一个向量x，它的转置矩阵可以通过将该向量转换为列向量，并将其转置得到。具体来说，如果向量x是一个n维向量，则其转置矩阵x^T是一个1行n列的矩阵，表示为：

x^T = [x1, x2, ..., xn]

其中，x1, x2, ..., xn分别表示向量x的第1个元素、第2个元素、...、第n个元素。

例如，如果向量x是一个3维向量，表示为：

x = [1, 2, 3]

则其转置矩阵x^T是一个1行3列的矩阵，表示为：

x^T = [1, 2, 3]

需要注意的是，向量的转置矩阵只有在进行矩阵乘法时才有意义，而在其他情况下，向量和其转置矩阵是等价的。

到此，以上就是小编对于写出设计矩阵X和因变量向量的问题就介绍到这了，希望介绍的3点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。